最小生成树

什么是最小生成树？

设定一个n点m条边的无向图G=(V,E)，V表示图中点的集合，E表示图中边的集合，n=|V|，m=|E|。

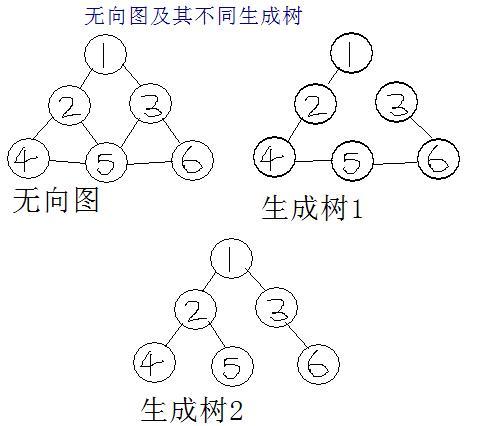
由V中的n个顶点和E中的n-1条边构成的无向连通子图成为G的一棵生成树，其中边权之和最小的生成树成为最小生成树。

Prim算法

与Dijkstra算法相似，prim算法也分为朴素版和堆优化版，而堆优化版一般使用不多。

Prim算法也分为以下几步，只不过这里的dist数组意义不同，dijkstra算法的dist数组的含义是距离起点的距离，而prim算法里的dist数组含义是距离集合的最短距离（即到集合内任何一点的距离最小值）：

1.进行n轮循环，每一轮循环中遍历所有的点，找到一个距离集合最小的点t。对于第一轮循环，因为dist全为INF，所以就是随机找一个点将dist初始化为0。

2.将找到的点t加入到集合当中，并且将生成树的总边权res更新。

3.用该点更新所有的dist。

因为这种方法一定可以遍历到所有的点，当某一个点t的dist为INF且不是第一轮时，代表这个点t与集合是不连通的，即不满足生成树的概念，不是连通的。

#include <bits/stdc++.h>
using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];
int dist[N];
bool st[N];

int prim()
{
    memset(dist, 0x3f, sizeof dist);

    int res = 0;
    for (int i = 0; i < n; i ++ ){
        int t = -1;

        for (int j = 1; j <= n; j ++ ){
            if (!st[j] && (t == -1 || dist[t] > dist[j]))
            t = j;
        }

        if (i && dist[t] == INF) return INF;

        if (i) res += dist[t];
        st[t] = true;

        for (int j = 1; j <= n; j ++ ) dist[j] = min(dist[j], g[t][j]);
    }

    return res;
}

int main()
{
    cin >> n >> m;

    memset(g, 0x3f, sizeof g);

    while (m -- ){
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c); // 无向图
    }

    int t = prim();

    if (t == INF) printf("impossible");
    else printf("%d\n", t);

    return 0;
}

Kruskal算法

Kruskal算法的思路十分简单，总体概括为以下两步。

1.将所有边按权重从小到大排序。

2.按权重大小枚举每条边ab，如果ab不连通，就将这条边加入到集合中。这部分的操作可以使用并查集来做。

#include <bits/stdc++.h>
using namespace std;

const int N = 100010, M = 200010, INF = 0x3f3f3f3f;

int n, m;
int p[N];

struct Edge
{
    int a, b, w;
}edges[M];

bool cmp(Edge a, Edge b)
{
    return a.w < b.w;
}

int find (int x)
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int kruskal()
{
    sort(edges, edges + m, cmp);

    for (int i = 0; i <= n; i ++ ) p[i] = i; // 并查集的初始操作

    int res = 0, cnt = 0; // cnt表示连通的边数
    for (int i = 0; i < m; i ++ ){
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;

        a = find(a), b = find(b);
        if (a != b){
            p[a] = b; // 将边加入集合
            res += w;
            cnt ++ ;
        }
    }
    if (cnt < n - 1) return INF;
    return res;
}

int main()
{
    cin >> n>> m;

    for (int i = 0; i < m; i ++ ){
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }

    int t = kruskal();

    if (t == INF) printf("impossible");
    else printf("%d", t);

    return 0;
}

关于Kruskal的拓展

Kruskal重构树：
在进行Kruskal的过程中，我们找到不在同一集合的两个边，不再合并两个点，而是新建一个节点，将该节点作为中转连接这两个集合，用这两个节点的边权作为该点的点权。

试想，如果我们按降序排序（从大到小）排序所有的边，再建Kruskal重构树，那么我们所建立的将是一个小根堆（因为最大的边总是先入，最后进入的一定是生成树内最小的边）。我们可以应用于从u出发只经过边权不超过x的边所能到达的节点。

对于最大重构树上的某lca(u,v)，其点权表示的是从u到v中最大边权的最小值。

重构树的构建

void kruskal()
{
    for(int i=1;i<=n;++i)ff[i]=i;
    sort(rem+1,rem+1+m,cmp);
    for(int i=1;i<=m;++i)
    {
        int fu=find(rem[i].u),fv=find(rem[i].v);
        if(fu!=fv)
        {
            val[++cnt]=rem[i].dis; // 用边权代表点权
            ff[cnt]=ff[fu]=ff[fv]=cnt; // 三点都加入集合
            add(fu,cnt); add(cnt,fu); // 建无向边
            add(fv,cnt); add(cnt,fv);
        }
    }
    for(int i=1;i<=cnt;++i)
    if(!vis[i])
    {
        int f=find(i);
        dfs1(f,0); dfs2(f,f);
    }
}