单调队列优化DP
单调队列优化的经典问题是滑动窗口,而滑动窗口本质上解决的问题都是移动区间内的最值问题,所以碰到此类问题我们都可以用单调队列进行优化。
纯滑动窗口问题
题目链接:154. 滑动窗口 - AcWing题库
#include <bits/stdc++.h>
using namespace std;
const int N = 1000010;
int a[N], q[N]; // q为单调队列,需要注意,队列中存放的是数组下标。
int main()
{
int n, k;
cin >> n >> k;
for (int i = 0; i < n; i ++ ) cin >> a[i];
int hh = 0, tt = -1; // hh为队列头,tt为队列尾。tt < hh的原因是防止在刚进入循环时判断出错,所以要将tt小于hh,从而达到先入一个数的情况。
for (int i = 0; i < n; i ++ ){ // 模拟队尾碰到新数a[i]的过程
if (hh <= tt && i - k + 1 > q[hh]) hh ++ ; // 单调队列长度大于k,队头出队,加上hh <= tt的原因主要是防止初始状态时tt < hh。
while (hh <= tt && a[q[tt]] >= a[i]) tt --; // 碰到新数a[i]后,若当前队尾大于a[i],则放入后不满足单调递减
q[ ++ tt] = i; // 新元素入队
if (i >= k - 1) printf("%d ", a[q[hh]]); // 用单调队列维护一个单调递减的区间,故每次窗口内最大值一定是队头
}
printf("\n");
// 以下同上,改为维护单调递增即可。
hh = 0, tt = -1;
for (int i = 0; i < n; i ++ ){
if (hh <= tt && i - k + 1 > q[hh]) hh ++ ;
while (hh <= tt && a[q[tt]] <= a[i]) tt --;
q[ ++ tt] = i;
if (i >= k - 1) printf("%d ", a[q[hh]]);
}
printf("\n");
return 0;
}考虑维护一个单调递增的前缀和的滑动窗口。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 300010;
int n, m;
int s[maxn], q[maxn];
int main () {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) {
cin >> s[i];
s[i] += s[i - 1]; // 前缀和
}
int res = -0x3f3f3f3f; // 长度至少为1
int hh = 0, tt = 0;
for (int i = 1; i <= n; i ++ ) { // 枚举右端点
if (q[hh] < i - m) hh ++ ; // 区间长度如果大于m,就不可以
res = max (res, s[i] - s[q[hh]]); // 更新最值
while (hh <= tt && s[i] <= s[q[tt]]) tt -- ; // 滑动窗口开滑
q[ ++ tt ] = i; // 入队
}
cout << res << endl;
}首先我们要考虑将环形问题化为一条区间。
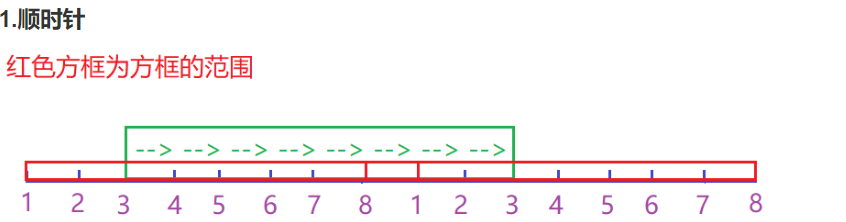
用p[i] 表示
如图,对于顺时针遍历,如果我们可以满足条件,从3走到3,那么对于所有的k,都存在s[k] - s[i] >= 0,即对图中情况,都满足s[k] - s[2] >= 0,即s[k] >= s[2]。所以我们只需要找到一个长度为n的滑动窗口,满足窗口内的最小值满足s[min] >= s[2],所以该题就转化为了一个区间最值问题。
同理逆时针

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 2e6 + 10;
int n;
int p[maxn], d[maxn];
int s[maxn];
int q[maxn];
bool st[maxn];
signed main () {
cin >> n;
for (int i = 1; i <= n; i ++ ) {
cin >> p[i] >> d[i];
}
for (int i = 1; i <= n; i ++ ) s[i] = s[i + n] = p[i] - d[i];
for (int i = 1; i <= 2 * n; i ++ ) s[i] += s[i - 1];
int hh = 0, tt = -1;
for (int i = 2 * n; i >= 1; i -- ) {
if (hh <= tt && q[hh] > i + n - 1) hh ++ ;
while (hh <= tt && s[q[tt]] >= s[i]) tt -- ;
q[ ++ tt] = i;
if (i <= n && s[q[hh]] >= s[i - 1]) st[i] = 1;
}
// 逆时针
hh = 0, tt = -1;
d[0] = d[n];
for (int i = 1; i <= n; i ++ ) s[i] = s[i + n] = p[i] - d[i - 1];
for (int i = 2 * n; i >= 0; i -- ) s[i] += s[i + 1];
for (int i = 1; i <= 2 * n; i ++ ) {
if (hh <= tt && q[hh] < i - n + 1) hh ++ ;
while (hh <= tt && s[q[tt]] >= s[i]) tt -- ;
q[ ++ tt] = i;
if (i > n && s[q[hh]] >= s[i + 1]) st[i - n] = 1;
}
for (int i = 1; i <= n; i ++ ) {
if (st[i]) cout << "TAK" << endl;
else cout << "NIE" << endl;
}
}滑动窗口+DP
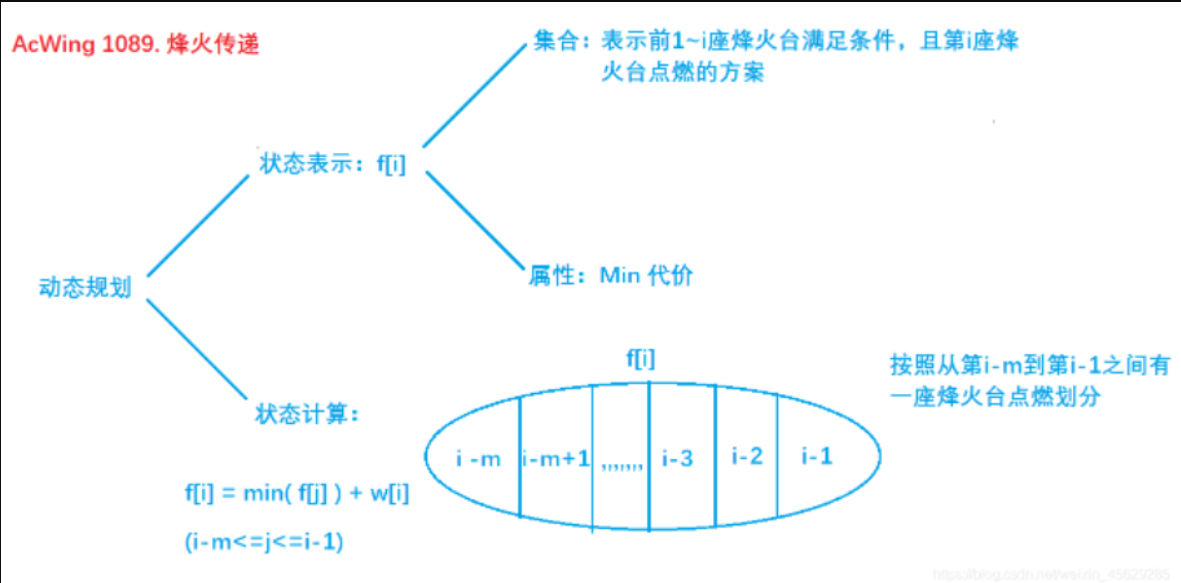
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 10, inf = -0x3f3f3f3f;
int n, m, l, r;
int a[maxn], f[maxn], q[maxn << 1];
int main () {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> a[i];
int hh = 0, tt = 0;
for (int i = 1; i <= n; i ++ ) {
if (q[hh] < i - m) hh ++ ;
f[i] = f[q[hh]] + a[i];
while (hh <= tt && f[q[tt]] >= f[i]) tt -- ;
q[ ++ tt] = i;
}
int res = 1e9;
for (int i = n - m + 1; i <= n; i ++ ) { // 答案一定在最后一段区间内选出
res = min(res, f[i]);
}
cout << res << endl;
}加入二分的做法。
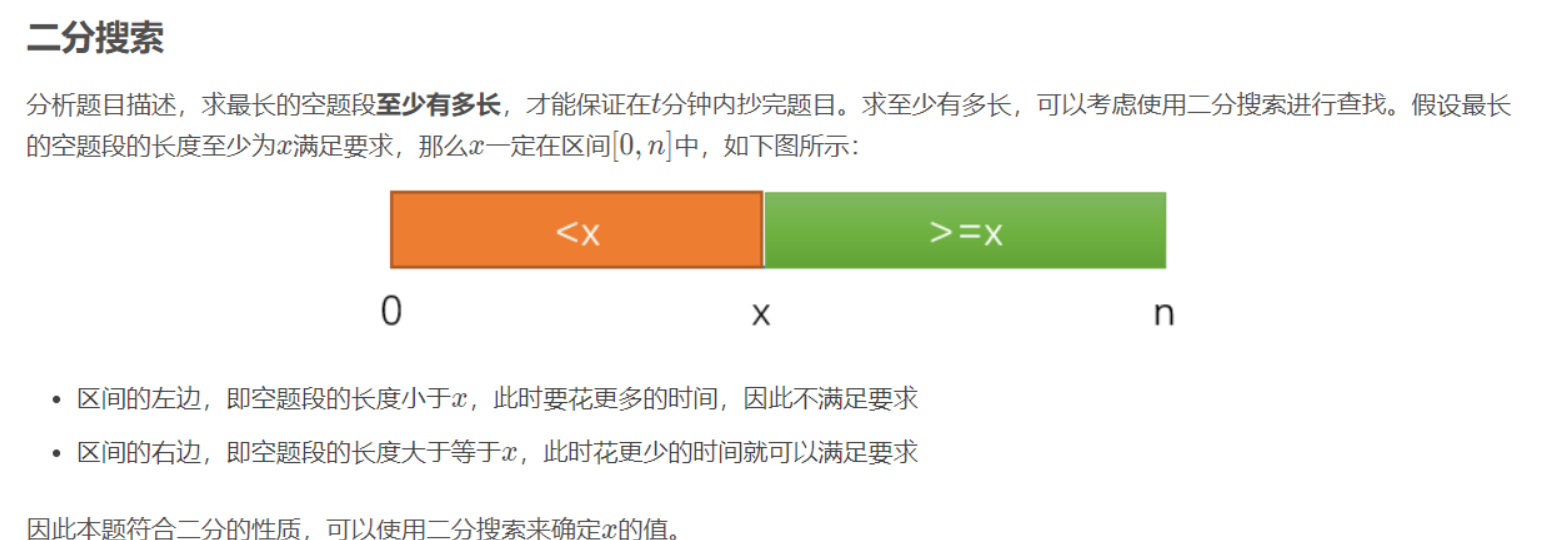
#include <bits/stdc++.h>
using namespace std;
const int maxn = 500100;
int n, m;
int w[maxn];
int q[maxn], f[maxn];
bool check (int x) {
int hh = 0, tt = 0;
for (int i = 1; i <= n; i ++ ) {
if (q[hh] < i - x - 1) hh ++ ;
f[i] = f[q[hh]] + w[i];
while (hh <= tt && f[q[tt]] >= f[i]) tt -- ;
q[ ++ tt ] = i;
}
for (int i = n - x; i <= n; i ++ ) {
if (f[i] <= m) return true;
}
return false;
}
int main () {
cin >> n >> m;
for (int i = 1; i <= n; i ++ ) cin >> w[i];
int l = 0, r = n;
while (l < r) {
int mid = l + r >> 1;
if (check(mid)) r = mid;
else l = mid + 1;
}
cout << l << endl;
}经典问题修剪草坪,我们可以把问题转化为每k+1头牛里至少选择一头,每次选择k+1内的最小值,这样就转化成了滑动窗口的裸题。
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int maxn = 1000010;
int q[maxn], n, m;
int ans, f[maxn];
signed main () {
cin >> n >> m;
int alls = 0;
for (int i = 1; i <= n; i ++ ) cin >> f[i], alls += f[i];
int hh = 0, tt = 0;
for (int i = 1; i <= n; i ++ ) {
if (hh <= tt && i - q[hh] > m + 1) hh ++ ;
f[i] += f[q[hh]];
while (hh <= tt && f[q[tt]] >= f[i]) tt -- ;
q[ ++ tt] = i;
}
for (int i = n - m; i <= n; i ++ ) ans = max(ans, alls - f[i]);
cout << ans << endl;
}二维滑动窗口
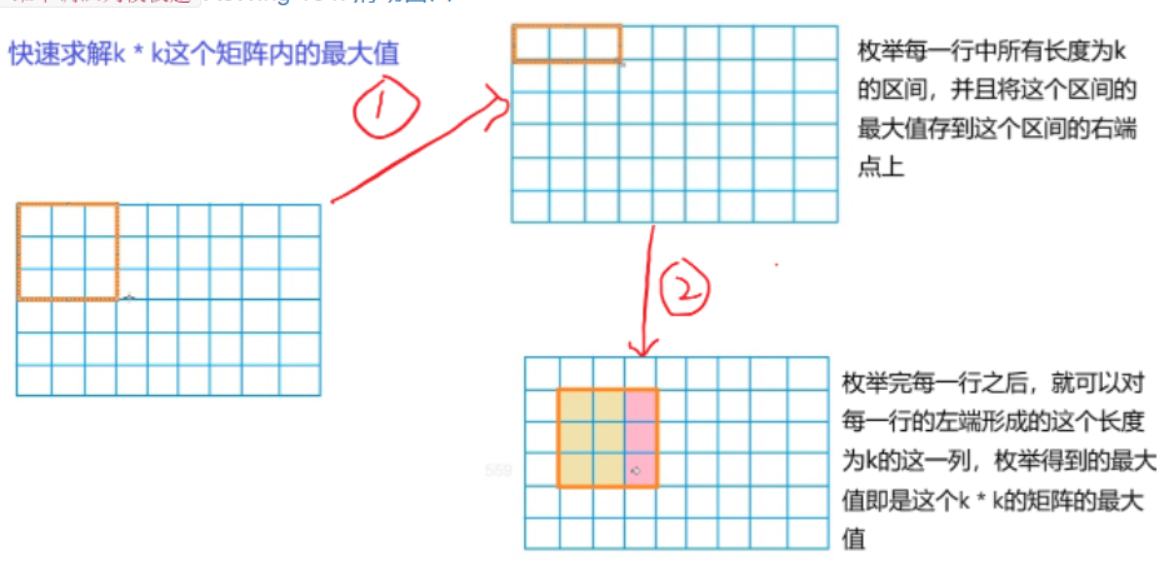
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
//#define int long long
const int maxn = 1010, inf = 1e9;
int n, m, k;
int w[maxn][maxn];
int row_min[maxn][maxn], row_max[maxn][maxn];
int q[maxn];
void get_min(int a[], int b[], int tot) {
int hh = 0, tt = -1;
for (int i = 1; i <= tot; i ++ ) {
if (hh <= tt && q[hh] <= i - k) hh ++ ;
while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;
q[ ++ tt] = i;
b[i] = a[q[hh]];
}
}
void get_max(int a[], int b[], int tot) {
int hh = 0, tt = -1;
for (int i = 1; i <= tot; i ++ ) {
if (hh <= tt && q[hh] <= i - k) hh ++ ;
while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;
q[ ++ tt] = i;
b[i] = a[q[hh]];
}
}
signed main () {
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n >> m >> k;
for (int i = 1; i <= n; i ++ ) {
for (int j = 1; j <= m; j ++ ) {
cin >> w[i][j];
}
}
for (int i = 1; i <= n; i ++ ) {
get_min(w[i], row_min[i], m);
get_max(w[i], row_max[i], m);
}
int res = inf;
int a[maxn], b[maxn], c[maxn];
for (int i = k; i <= m; i ++ ) {
for (int j = 1; j <= n; j ++ ) a[j] = row_min[j][i];
get_min(a, b, n);
for (int j = 1; j <= n; j ++ ) a[j] = row_max[j][i];
get_max(a, c, n);
for (int j = k; j <= n; j ++ ) res = min(res, c[j] - b[j]);
}
cout << res << endl;
}


